Um circuito RLC (também conhecido como circuito ressonante ou circuito aceitador) é um circuito elétrico consistindo de um resistor (R), um indutor (L), e um capacitor (C), conectados em série ou em paralelo.
O circuito RLC é chamado de circuito de segunda ordem visto que qualquer tensão ou corrente nele pode ser descrita por uma equação diferencial de segunda ordem.
Alternativamente, para aplicações em filtros passa-banda, o factor de carga é escolhido baseado na largura de banda desejada do filtro. Para uma maior largura de banda, um maior factor de carga é necessário, e para uma largura de banda menor, utiliza-se um menor factor de carga. Na prática, isto requer ajustar os valores relativos da resistência R e do indutor L no circuito.
 nas frequências de metade da potência.
nas frequências de metade da potência.
Dados os parâmetros v, R, L, e C, a solução para a corrente (I) utilizando a Lei da Tensão de Kirchoff é:

Substituindo estes parâmetros na equação diferencial, obtém-se:
O primeiro já foi feito, visto que a corrente na total é igual à corrente no indutor, portanto
Duas raízes reais negativas, as soluções são:
As duas raízes são idênticas (λ1 = λ2 = λ). As soluções são:
As soluções consistem de duas raízes conjugadas
 ], pode-se simplificar a solução para
], pode-se simplificar a solução para
Suponha v(t) = Au(t)
Para encontrar a solução mais facilmente começa-se resolvendo-a para a função de passo Heaviside e então utilizando o facto de que o nosso circuito é um sistema linear, a sua derivada será a solução para a função delta.
A equação então será, para t>0:
 ), a solução é:
), a solução é:
 :
:
Note que existe um pico em Imag(ω) = 1. Este é conhecido como a frequência de ressonância. Resolvendo para este valor, encontra-se:
Para uma configuração paralelo dos mesmos componentes, aonde Φ é o fluxo magnético no sistema, tem-se abaixo:


O circuito RLC é chamado de circuito de segunda ordem visto que qualquer tensão ou corrente nele pode ser descrita por uma equação diferencial de segunda ordem.
Parâmetros fundamentais
Existem dois parâmetros fundamentais que descrevem o comportamento dos circuitos RLC: a frequência de ressonância e o factor de carga. Para além disso, existem outros parâmetros que podem ser derivados destes dois primeiros.Frequência de ressonância
A frequência natural ou de ressonância sem carga de um circuito RLC (em radianos por segundo) é:-
- ZLC = ZL + ZC = 0
-

- ZL = Ls
Fator de carga
O fator de carga do circuito (em radianos por segundo) é:Alternativamente, para aplicações em filtros passa-banda, o factor de carga é escolhido baseado na largura de banda desejada do filtro. Para uma maior largura de banda, um maior factor de carga é necessário, e para uma largura de banda menor, utiliza-se um menor factor de carga. Na prática, isto requer ajustar os valores relativos da resistência R e do indutor L no circuito.
Parâmetros derivados
Os parâmetros derivados incluem largura de banda, fator Q e frequência de ressonância com carga.Largura de banda
O circuito RLC pode ser utilizado como um filtro passa-faixa ou rejeita-faixa, e a sua largura de banda (em radianos por segundo) é: nas frequências de metade da potência.
nas frequências de metade da potência.Qualidade ou factor Q
A qualidade do circuito, ou factor Q (ver Equalizador), é calculada como a razão entre a frequência de ressonância ωo e a largura de banda Δω (em radianos por segundo):Ressonância com carga
A frequência de ressonância com carga deriva da frequência de ressonância natural e do factor de carga. Se o circuito estiver com subcarga, verifica-se que .
.
 (approx).
(approx).
Configurações
Todo circuito RLC consiste de dois componentes: uma fonte de alimentação e um ressonador. Existem dois tipos de fontes de alimentação, a fonte de Thévenin e a fonte de Norton. Da mesma forma, existem dois tipos de ressonadores, os LC série e o LC paralelo. Como resultado, existem quatro configurações de circuitos RLC:- LC série com fonte de alimentação do tipo Thévenin
- LC série com fonte de alimentação do tipo Norton
- LC paralelo com fonte de alimentação do tipo Thévenin
- LC paralelo com fonte de alimentação do tipo Norton
Análise do circuito
RLC série com fonte da alimentação do tipo Thévenin
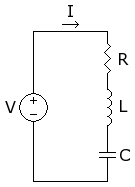
Neste circuito, os três componentes estão todos em série com a fonte de tensão.Notações do circuito RLC série:
|

-
- e
Substituindo estes parâmetros na equação diferencial, obtém-se:
A solução para Resposta de Entrada Zero (ZIR)
Colocando a entrada (fonte de tensão) em zero, obtém-se:O primeiro já foi feito, visto que a corrente na total é igual à corrente no indutor, portanto
Sobrecarga/Regime sobreamortecido (aperiódico)
Duas raízes reais negativas, as soluções são:
Carga crítica/ Regime amortecido crítico (aperiódico limite)
As duas raízes são idênticas (λ1 = λ2 = λ). As soluções são:
- I(t) = (A + Bt)eλt
- para constantes arbitrárias A e B
Subcarga/ Regime subamortecido (periódico amortecido; pseudo-periódico)
As soluções consistem de duas raízes conjugadas
-
- λ1 = − ζ + iωc
-
- λ2 = − ζ − iωc
-
- para constantes arbitrárias A e B.
 ], pode-se simplificar a solução para
], pode-se simplificar a solução para-
- para constantes arbitrárias C e D.
Solução para Resposta de Estado Zero (ZSR)
Com as condições iniciais configuradas para zero e utilizando a seguinte equação:Transformada de Laplace
Primeiramente realiza-se a transformada de Laplace da equação diferencial de segunda ordem:-
- onde V(s) é a transformada de Laplace do sinal de entrada:
Suponha v(t) = Au(t)
-
- onde u(t) é a função de passo Heaviside.
Integral de convolução
Uma solução separada para cada função possível para V(t) é impossível. No entanto, existe um método para encontrar uma fórmula para I(t) utilizando a convolução. Para fazer isto, é necessário uma solução para uma entrada básica, a função delta de Dirac.Para encontrar a solução mais facilmente começa-se resolvendo-a para a função de passo Heaviside e então utilizando o facto de que o nosso circuito é um sistema linear, a sua derivada será a solução para a função delta.
A equação então será, para t>0:
Sobrecarga
Neste caso temos duas raízes reais negativas, a solução é:Carga crítica
Nesta caso, as raízes são idênticas (λ1 = λ2 = λ), a solução é:Subcarga
Neste caso existem duas raízes complexas conjugadas ( ), a solução é:
), a solução é:Domínio da frequência
O circuito RLC série pode ser analisado no domínio da frequência utilizando as relações de impedância complexa. Se a fonte de tensão acima produz uma forma de onda exponencial complexa com a amplitude V(s) e frequência angular s = σ + iω, a Lei de Kirchoff para Tensão pode ser aplicada:Admitância complexa
A seguir, a resolução para a admitância complexa Y(s):Pólos e Zeros
Os zeros de Y(s) são os valores de s tais que Y(s) = 0:-
- s = 0 e

- s = 0 e
 :
:Estado sinusoidal constante
Supondo s = iω, obtendo a magnitude da equação acima obtém-se:Note que existe um pico em Imag(ω) = 1. Este é conhecido como a frequência de ressonância. Resolvendo para este valor, encontra-se:
Circuito RLC paralelo
Um modo de recuperar as propriedades do circuito RLC é através do uso da não-dimensionalização. | Notações do circuito RLC paralelo:
|








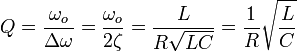








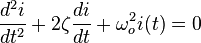



![\Rightarrow i'(0)={1 \over L}\left[-v_C(0)-I(0)R \right]](http://upload.wikimedia.org/math/e/6/e/e6e20bf78dcfa3cb2b1deee36622a62a.png)

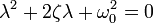



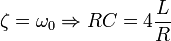

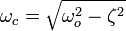

![i(t)=e^{-\zeta t} \left[ C \sin(\omega_c t) + D \cos(\omega_c t) \right]](http://upload.wikimedia.org/math/0/e/8/0e8c8f3e87939aaaa547a29330fe5612.png)





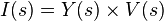





![I_u(t)={1 \over {L(\lambda_1-\lambda_2)}} \left[ e^{\lambda_1 t}-e^{\lambda_2 t} \right]](http://upload.wikimedia.org/math/5/e/9/5e97294de664bf98681881d92e7a8be4.png)
![\Rightarrow I_{\delta}(t)={1 \over {L(\lambda_1-\lambda_2)}} \left[ \lambda_1 e^{\lambda_1 t}-\lambda_2 e^{\lambda_2 t} \right]](http://upload.wikimedia.org/math/5/c/d/5cdb527c2051670cf7a6cf61f7cfc42e.png)


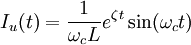
![\Rightarrow I_{\delta}(t)={1 \over {\omega_c L}} e^{\zeta t} \left[ \zeta \sin(\omega_c t) + \omega_c \cos(\omega_c t) \right]](http://upload.wikimedia.org/math/5/c/1/5c1c34fe44c3fc9562af386325218dfa.png)










Nenhum comentário:
Postar um comentário